曲面的切平面
给出一个曲面的参数方程:
r[u_, v_] := {x[u, v], y[u, v], z[u, v]};
那么,当u为变量,而v为定值的时候,r[u, v] 就变成了一条曲线,这条曲线恰好就是曲面的网格线里面的u曲线。
同样的,当v为变量,而u为定值的时候,r[u, v] 就变成了曲面的网格线里面的v曲线。
以如下曲面为例:
r[u_, v_] := {Cos[u] Cos[v]^2, Cos[u] Sin[v]^2, Sin[u] Cos[v]}
ParametricPlot3D[r[u, v], {u, 0, 2 Pi}, {v, 0, Pi}]
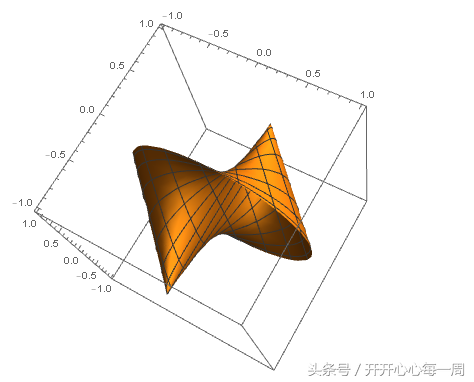
我们隐藏这个曲面的网格线:
ParametricPlot3D[r[u, v], {u, 0, 2 Pi}, {v, 0, Pi}, Mesh -> None]
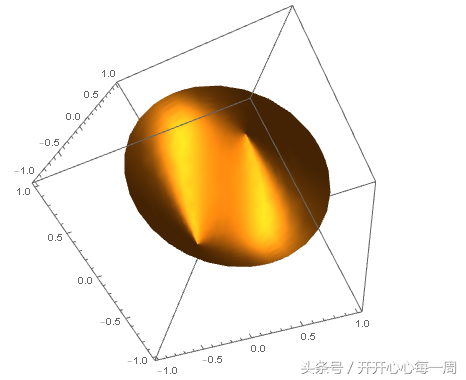

单独把u曲线族绘制出来:

单独把v曲线族绘制出来:
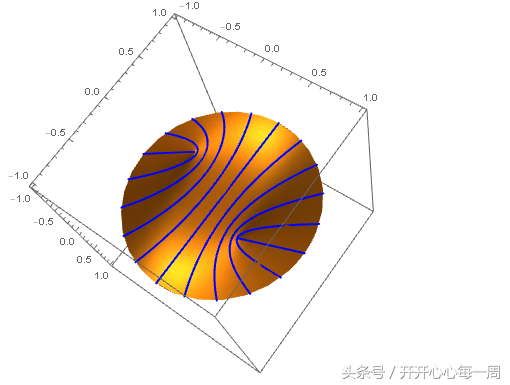
把u曲线族和v曲线族画到一起:
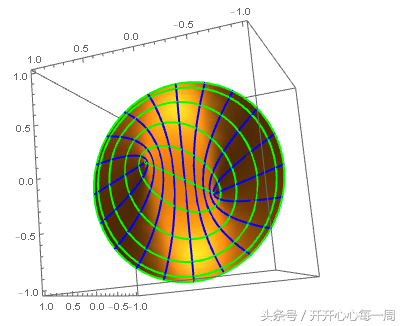
这样,{u,v} 就确定了曲面上每一个点的坐标,由此可以看出,三维空间里的曲面,其实是二维曲面。这里顺便提一下,庞加莱大猜想里面提到的三维球面,指的是四维空间里面四维球体的边界。
看一下,曲面上 "原点" 的位置在哪里:
Show[ParametricPlot3D[r[u, v], {u, 0, 2 Pi}, {v, 0, Pi}, Mesh -> None],Graphics3D[{Red, PointSize -> 0.05, Point[r[0, 0]]}]]
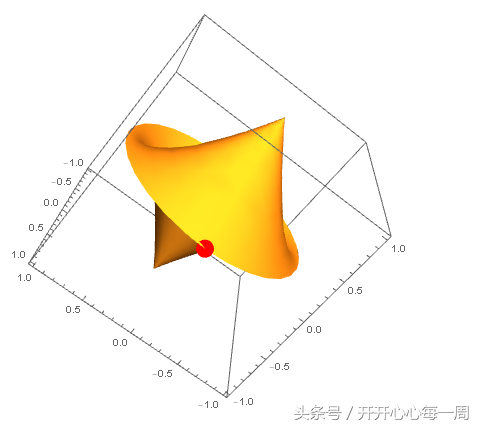
可以看到,曲面的 "原点" 在边缘线上。注意,如果是封闭的曲面,就没有所谓的边缘线了。
绘制一条过原点的u曲线:
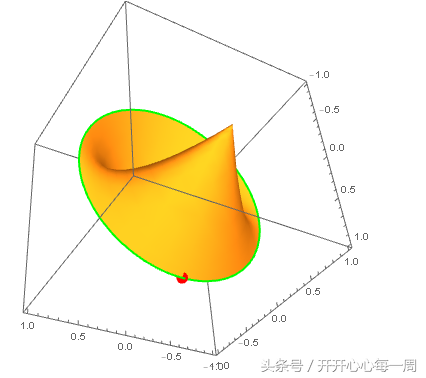
画出这条u曲线在原点的切向量:
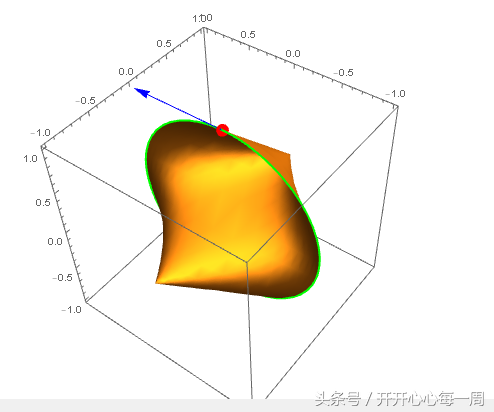
在上图的基础上,加上一条过原点的v曲线:

注意看这条v曲线,其实是折线段,而原点恰好位于折点的位置,所以没有切向量。
没有了v曲线的切向量,也就没有了曲面在原点处的切平面。
我们需要找一个有切平面的点,就不能是边缘线上的点,也不能是尖点。
碰碰运气,看看点 {1/2 + \[Pi], \[Pi]/3} 的位置:
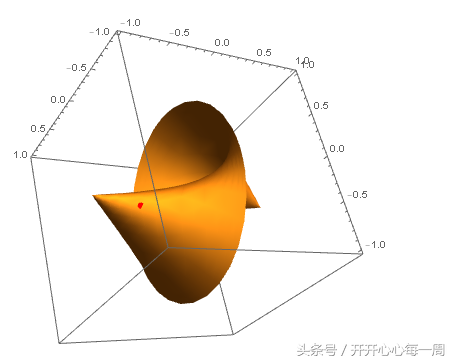
这个点应该存在切平面了吧。先画出过这个点的u曲线和v曲线在该点的切向量:
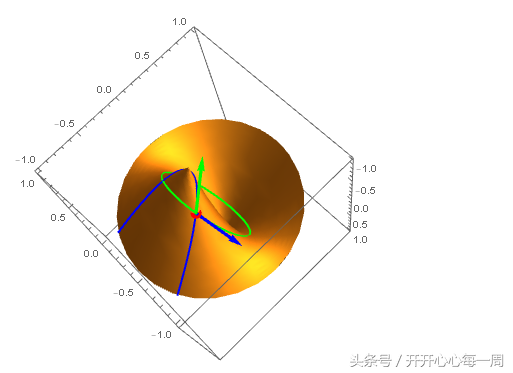
再画出过这个点的另一条曲线:
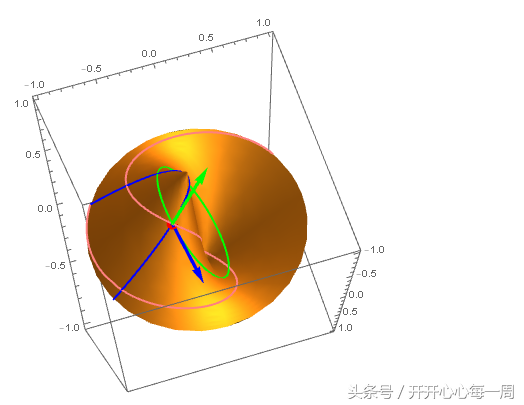
可以看到,这条粉色曲线七拐八绕,很复杂,它也过点 {1/2 + \[Pi], \[Pi]/3},而且在这个点上也有切向量:
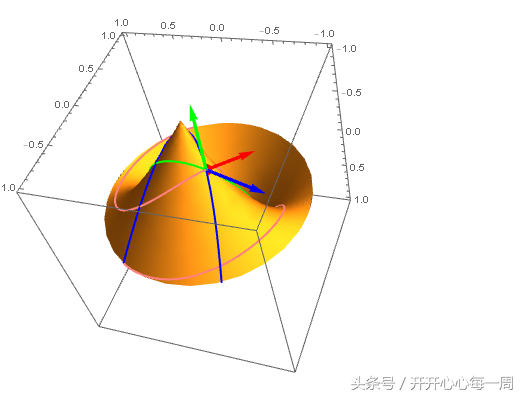
可以证明,这三个向量是共面的:
Det[{D[r[u, Pi/3], u] /. u -> 1/2 + Pi,
D[r[1/2 + Pi, v], v] /. v -> Pi/3,
D[r[u, v] /. u -> 3 v + 1/2, v] /. v -> Pi/3}]
运行结果是0。
注意:虽然三维空间里的曲面都属于而二维曲面,但是作为三维空间的子元素,曲面上每一个点都保留了三维的属性。


